even root|even root vs odd root : iloilo When we are given the equation of a function f(x), we can check whether the function is even, odd, or neither by evaluating f(-x). If we get an expression that is equivalent to f(x), we have an even function; if we get an expression that is equivalent to -f(x), .
Watch hottest collections of Most viewed videos on PinayFlix for free. Pinay Flixx. Home; What's Hot. Latest; Popular; Most Viewed Pinay College ; Pinay Model ; Showbiz ; Confessions ; Viral / Trending . Most viewed videos. HD. 100% . 10.37K. Gumamit ng Pilik-Mata ng Kambing Para Lalo Mapatirik. HD. 100% . 18.66K. Get A Girl na Bigla .
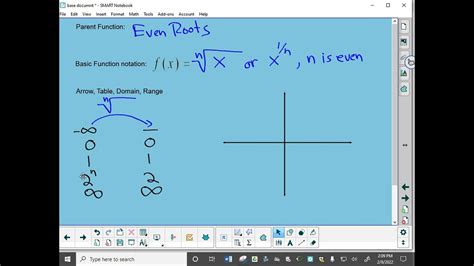
even root,An even root refers to taking the root (or extracting the root) of an expression with an even index. Specifically, an even root refers to square roots ( ), fourth roots ( 4 ), sixth . Learn how to classify and find the domain of a root function with an even index, such as a square root. See examples, definitions, and inequalities for even roots. The difference between odd and even roots, how a real number has just one real cube root, how an even index number or even root has TWO possible answers if the radicand is positive, and how to.

The n n -th root of the number a a is defined as follows: Case I: n n is an odd number. In this case the nth n th root of a a is defined to be that number b ∈R b ∈ R such that bn = .
This video shows the basic characteristics of a radical function. It shows what effects the even root's domain and range. It shows what is so odd about an odd root. .more. When we are given the equation of a function f(x), we can check whether the function is even, odd, or neither by evaluating f(-x). If we get an expression that is equivalent to f(x), we have an even function; if we get an expression that is equivalent to -f(x), .
even root vs odd root Definition: SIMPLIFYING ODD AND EVEN ROOTS. For any integer \(n \ge 2\), \[\begin{array}{cc} {\text{when n is odd}}&{\sqrt[n]{a^n}=a}\\ {\text{when n is .
even root Solving Equations with Rational Exponents. When exponents are fractions, we convert the rational exponent into a radical expression to solve. Recall, \ (a^ {\dfrac .
even root even root vs odd root Find the domain of f of x is equal to the principal square root of 2x minus 8. So the domain of a function is just the set of all of the possible valid inputs into the function, or all of the possible values for which the function is defined. When \(n\) is an even number and: \(a \geq 0\), then \(\sqrt[n]{a}\) is a real number. \(a<0\), then \(\sqrt[n]{a}\) is not a real number. When \(n\) is an odd number, .
The square root function is \(f(x)=\sqrt{x}\). . For a radical with an even index, we said the radicand had to be greater than or equal to zero as even roots of negative numbers are not real numbers. For an odd index, the radicand can be any real number. We restate the properties here for reference. The Even Root Property. With even roots, we have the restriction on the radicand where the radicand is required to be non-negative here. We discussed this in the previous section, e.g., \(\sqrt{-4}\) is not a real number. We continue this restriction when taking even roots of an equation. Figure 8.1.1. The square root of m, √m, is a positive number whose square is m. nth Root of a Number. If bn = a, then b is an nth root of a. The principal nth root of a is written n√a. n is called the index of .For the odd and even nature of roots, (repeating the above) there are three cases: p is even, and q is odd. p is odd and q is even. p is odd and q is odd. In case 1: p 2 (even)+pq (even)+q 2 (odd)=e+e+o=0 (e) This is not possible, because an odd number would equal an even number. In case 2:

Add an even mixture of milk and cream. أضيفي الحليب والقشطة بنسب متساوية. even adj. (sports: tied) متعادل. She was winning a moment ago but now they're even. كانت هي في الطليعة قبل لحظات ولكنهما الآن متعادلتان. even adj. (number: divisible by two) (عدد) Example 8.8.5. Find the domain of the function, g(x) = √ 6 x − 1. Write the domain in interval notation. Solution: Solve the function, g(x) = √ 6 x − 1 has a radical with an index of 2, which is even, we know the radicand must be greater than or equal to 0. The radicand cannot be zero since the numerator is not zero.
Maybe you confused cube root with square root. Although even roots of negative numbers cannot be solved with just real numbers, odd roots are possible. For example: (-3)(-3)(-3)=cbrt(-27) Even though you are multiplying a negative number, it is . The same is true for any even root. Even roots of negative numbers are not real numbers. Odd roots of negative numbers are real numbers. Definition: PROPERTIES OF \(\sqrt[n]{a}\) When n is an even number and \(a\ge 0\), .
even root|even root vs odd root
PH0 · odd root definition
PH1 · how to rewrite cube root
PH2 · exponents and roots rules
PH3 · even roots of negative numbers
PH4 · even root vs odd root
PH5 · even root property calculator
PH6 · even root property
PH7 · even root function
PH8 · Iba pa